D'Alembert Force on:
[Wikipedia]
[Google]
[Amazon]
A fictitious force is a
/ref> D'Alembert's principle is just another way of formulating Newton's second law of motion. It defines an inertial force as the negative of the product of mass times acceleration, just for the sake of easier calculations. (A d'Alembert force is not to be confused with a
 The effect of a fictitious force also occurs when a car takes
The effect of a fictitious force also occurs when a car takes
 As a related example, suppose the moving coordinate system ''B'' rotates with a constant angular speed ω in a circle of radius ''R'' about the fixed origin of inertial frame ''A'', but maintains its coordinate axes fixed in orientation, as in Figure 3. The acceleration of an observed body is now (see Eq. 1):
:
where the summations are zero inasmuch as the unit vectors have no time dependence. The origin of the system ''B'' is located according to frame ''A'' at:
:
leading to a velocity of the origin of frame ''B'' as:
:
leading to an acceleration of the origin of ''B'' given by:
:
Because the first term, which is
is of the same form as the normal centrifugal force expression:
it is a natural extension of standard terminology (although there is no standard terminology for this case) to call this term a "centrifugal force". Whatever terminology is adopted, the observers in frame ''B'' must introduce a fictitious force, this time due to the acceleration from the orbital motion of their entire coordinate frame, that is radially outward away from the centre of rotation of the origin of their coordinate system:
:
and of magnitude:
:
This "centrifugal force" has differences from the case of a rotating frame. In the rotating frame the centrifugal force is related to the distance of the object from the origin of frame ''B'', while in the case of an orbiting frame, the centrifugal force is independent of the distance of the object from the origin of frame ''B'', but instead depends upon the distance of the origin of frame ''B'' from ''its'' centre of rotation, resulting in the ''same'' centrifugal fictitious force for ''all'' objects observed in frame ''B''.
As a related example, suppose the moving coordinate system ''B'' rotates with a constant angular speed ω in a circle of radius ''R'' about the fixed origin of inertial frame ''A'', but maintains its coordinate axes fixed in orientation, as in Figure 3. The acceleration of an observed body is now (see Eq. 1):
:
where the summations are zero inasmuch as the unit vectors have no time dependence. The origin of the system ''B'' is located according to frame ''A'' at:
:
leading to a velocity of the origin of frame ''B'' as:
:
leading to an acceleration of the origin of ''B'' given by:
:
Because the first term, which is
is of the same form as the normal centrifugal force expression:
it is a natural extension of standard terminology (although there is no standard terminology for this case) to call this term a "centrifugal force". Whatever terminology is adopted, the observers in frame ''B'' must introduce a fictitious force, this time due to the acceleration from the orbital motion of their entire coordinate frame, that is radially outward away from the centre of rotation of the origin of their coordinate system:
:
and of magnitude:
:
This "centrifugal force" has differences from the case of a rotating frame. In the rotating frame the centrifugal force is related to the distance of the object from the origin of frame ''B'', while in the case of an orbiting frame, the centrifugal force is independent of the distance of the object from the origin of frame ''B'', but instead depends upon the distance of the origin of frame ''B'' from ''its'' centre of rotation, resulting in the ''same'' centrifugal fictitious force for ''all'' objects observed in frame ''B''.
 As a combination example, Figure 4 shows a coordinate system ''B'' that orbits inertial frame ''A'' as in Figure 3, but the coordinate axes in frame ''B'' turn so unit vector u1 always points toward the centre of rotation. This example might apply to a test tube in a centrifuge, where vector u1 points along the axis of the tube toward its opening at its top. It also resembles the Earth–Moon system, where the Moon always presents the same face to the Earth.However, the Earth–Moon system rotates about its
As a combination example, Figure 4 shows a coordinate system ''B'' that orbits inertial frame ''A'' as in Figure 3, but the coordinate axes in frame ''B'' turn so unit vector u1 always points toward the centre of rotation. This example might apply to a test tube in a centrifuge, where vector u1 points along the axis of the tube toward its opening at its top. It also resembles the Earth–Moon system, where the Moon always presents the same face to the Earth.However, the Earth–Moon system rotates about its
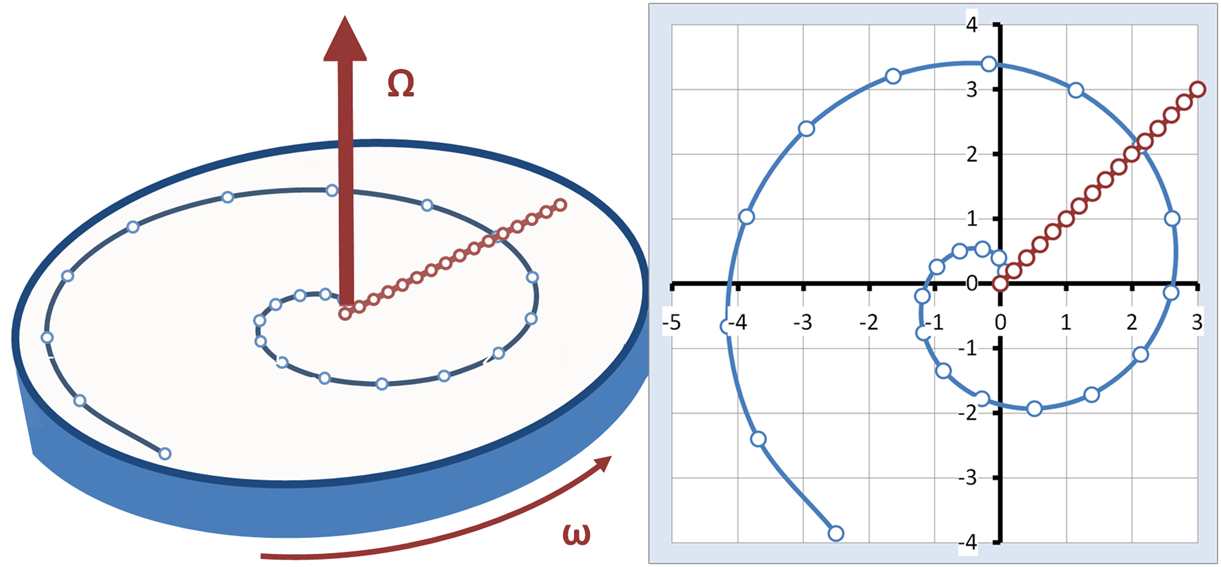 Figure 5 shows another example comparing the observations of an inertial observer with those of an observer on a rotating
Figure 5 shows another example comparing the observations of an inertial observer with those of an observer on a rotating
Q and A from Richard C. Brill, Honolulu Community College
* ttps://scienceworld.wolfram.com/physics/CoriolisForce.html Coriolis Force
Motion over a flat surface
Java physlet by Brian Fiedler illustrating fictitious forces. The physlet shows both the perspective as seen from a rotating and from a non-rotating point of view.
Java physlet by Brian Fiedler illustrating fictitious forces. The physlet shows both the perspective as seen from a rotating and as seen from a non-rotating point of view. {{Authority control Classical mechanics Force
force
In physics, a force is an influence that can change the motion of an object. A force can cause an object with mass to change its velocity (e.g. moving from a state of rest), i.e., to accelerate. Force can also be described intuitively as a p ...
that appears to act on a mass whose motion is described using a non-inertial frame of reference
A non-inertial reference frame is a frame of reference that undergoes acceleration with respect to an inertial frame. An accelerometer at rest in a non-inertial frame will, in general, detect a non-zero acceleration. While the laws of motion are ...
, such as a linearly accelerating or rotating reference frame
A rotating frame of reference is a special case of a non-inertial reference frame that is rotating relative to an inertial reference frame. An everyday example of a rotating reference frame is the surface of the Earth. (This article considers onl ...
.
It is related to Newton's second law of motion
Newton's laws of motion are three basic laws of classical mechanics that describe the relationship between the motion of an object and the forces acting on it. These laws can be paraphrased as follows:
# A body remains at rest, or in motion ...
, which treats forces for just one object.
Passengers in a vehicle accelerating in the forward direction may perceive they are acted upon by a force moving them into the direction of the backrest of their seats for example. An example in a rotating reference frame may be the impression that it is a force which seems to move objects outward toward the rim of a centrifuge or carousel.
The fictitious force called a pseudo force might also be referred to as a body force
In physics, a body force is a force that acts throughout the volume of a body.
Springer site - Book 'Solid mechanics'preview paragraph 'Body forces'./ref>
Forces due to gravity, electric fields and magnetic fields are examples of body forces. Bo ...
. It is due to an object's inertia
Inertia is the idea that an object will continue its current motion until some force causes its speed or direction to change. The term is properly understood as shorthand for "the principle of inertia" as described by Newton in his first law ...
when the reference frame does not move inertially any more but begins to accelerate relative to the free object. In terms of the example of the passenger vehicle, a pseudo force seems to be active just before the body touches the backrest of the seat in the car. A person in the car leaning forward first moves a bit backward in relation to the already accelerating car, before touching the backrest. The motion in this short period just seems to be the result of a force on the person, it's a pseudo force. A pseudo force does not arise from any physical interaction
In physics, the fundamental interactions, also known as fundamental forces, are the interactions that do not appear to be reducible to more basic interactions. There are four fundamental interactions known to exist: the gravitational and electrom ...
between two objects, such as electromagnetism
In physics, electromagnetism is an interaction that occurs between particles with electric charge. It is the second-strongest of the four fundamental interactions, after the strong force, and it is the dominant force in the interactions of a ...
or contact forces. It's just a consequence of the acceleration a of the physical object the non-inertial reference frame
A non-inertial reference frame is a frame of reference that undergoes acceleration with respect to an inertial frame. An accelerometer at rest in a non-inertial frame will, in general, detect a non-zero acceleration. While the laws of motion are ...
is connected to, i.e. the vehicle in this case. From the viewpoint of the respective accelerating frame, an acceleration of the inert object appears to be present, apparently requiring a "force" for this to have happened.
As stated by Iro:
The pseudo force on an object arises as an imaginary influence when the frame of reference used to describe the object's motion is accelerating compared to a non-accelerating frame. The pseudo force "explains," using Newton's second law mechanics, why an object does not follow Newton's second law and "floats freely" as if weightless. As a frame may accelerate in any arbitrary way, so may pseudo forces also be as arbitrary (but only in direct response to the acceleration of the frame).
An example of a pseudo force as defined by Iro is the Coriolis force
In physics, the Coriolis force is an inertial or fictitious force that acts on objects in motion within a frame of reference that rotates with respect to an inertial frame. In a reference frame with clockwise rotation, the force acts to the ...
, maybe better to be called: the Coriolis effect;
The gravitational force
In physics, gravity () is a fundamental interaction which causes mutual attraction between all things with mass or energy. Gravity is, by far, the weakest of the four fundamental interactions, approximately 1038 times weaker than the strong ...
would also be a fictitious force (pseudo force), based upon a field model in which particles distort spacetime
In physics, spacetime is a mathematical model that combines the three dimensions of space and one dimension of time into a single four-dimensional manifold. Spacetime diagrams can be used to visualize relativistic effects, such as why differen ...
due to their mass, such as in the theory of general relativity
General relativity, also known as the general theory of relativity and Einstein's theory of gravity, is the geometric theory of gravitation published by Albert Einstein in 1915 and is the current description of gravitation in modern physics ...
.
Assuming Newton's second law
Newton's laws of motion are three basic laws of classical mechanics that describe the relationship between the motion of an object and the forces acting on it. These laws can be paraphrased as follows:
# A body remains at rest, or in motion ...
in the form F = ''m''/ref> D'Alembert's principle is just another way of formulating Newton's second law of motion. It defines an inertial force as the negative of the product of mass times acceleration, just for the sake of easier calculations. (A d'Alembert force is not to be confused with a
contact force
A contact force is any force that occurs as a result of two objects making contact with each other. Contact forces are ubiquitous and are responsible for most visible interactions between macroscopic collections of matter. Pushing a car or kickin ...
arising from the physical interaction between two objects, which is the subject of Newton's third law – 'action is reaction
Reaction may refer to a process or to a response to an action, event, or exposure:
Physics and chemistry
*Chemical reaction
*Nuclear reaction
*Reaction (physics), as defined by Newton's third law
*Chain reaction (disambiguation).
Biology and me ...
'.
In terms of the example of the passenger vehicle above, a contact force emerges when the body of the passenger touches the backrest of the seat in the car. It is present for as long as the car is accelerated.)
Four fictitious forces have been defined for frames accelerated in commonly occurring ways:
* one caused by any acceleration relative to the origin in a straight line (rectilinear acceleration
In mechanics, acceleration is the rate of change of the velocity of an object with respect to time. Accelerations are vector quantities (in that they have magnitude and direction). The orientation of an object's acceleration is given by the ...
);
* two involving rotation: centrifugal force
In Newtonian mechanics, the centrifugal force is an inertial force (also called a "fictitious" or "pseudo" force) that appears to act on all objects when viewed in a rotating frame of reference. It is directed away from an axis which is paralle ...
and Coriolis effect
In physics, the Coriolis force is an inertial or fictitious force that acts on objects in motion within a frame of reference that rotates with respect to an inertial frame. In a reference frame with clockwise rotation, the force acts to the ...
* and a fourth, called the Euler force In classical mechanics, the Euler force is the fictitious tangential force
that appears when a non-uniformly rotating reference frame is used for analysis of motion and there is variation in the angular velocity of the reference frame's axes. The E ...
, caused by a variable rate of rotation, should that occur.
Background
The role of fictitious forces in Newtonian mechanics is described by Tonnelat: Fictitious forces arise inclassical mechanics
Classical mechanics is a physical theory describing the motion of macroscopic objects, from projectiles to parts of machinery, and astronomical objects, such as spacecraft, planets, stars, and galaxies. For objects governed by classical ...
and special relativity
In physics, the special theory of relativity, or special relativity for short, is a scientific theory regarding the relationship between space and time. In Albert Einstein's original treatment, the theory is based on two postulates:
# The laws o ...
in all non-inertial frames.
Inertial frames are privileged over non-inertial frames because they do not have physics whose causes are outside of the system, while non-inertial frames do. Fictitious forces, or physics whose cause is outside of the system, are no longer necessary in general relativity
General relativity, also known as the general theory of relativity and Einstein's theory of gravity, is the geometric theory of gravitation published by Albert Einstein in 1915 and is the current description of gravitation in modern physics ...
, since these physics are explained with the geodesics
In geometry, a geodesic () is a curve representing in some sense the shortest path ( arc) between two points in a surface, or more generally in a Riemannian manifold. The term also has meaning in any differentiable manifold with a connection. ...
of spacetime
In physics, spacetime is a mathematical model that combines the three dimensions of space and one dimension of time into a single four-dimensional manifold. Spacetime diagrams can be used to visualize relativistic effects, such as why differen ...
: "The field of all possible space-time null geodesics or photon paths unifies the absolute local non-rotation standard throughout space-time.".
On Earth
The surface of the Earth is arotating reference frame
A rotating frame of reference is a special case of a non-inertial reference frame that is rotating relative to an inertial reference frame. An everyday example of a rotating reference frame is the surface of the Earth. (This article considers onl ...
. To solve classical mechanics
Classical mechanics is a physical theory describing the motion of macroscopic objects, from projectiles to parts of machinery, and astronomical objects, such as spacecraft, planets, stars, and galaxies. For objects governed by classical ...
problems exactly in an Earthbound reference frame, three fictitious forces must be introduced: the Coriolis force
In physics, the Coriolis force is an inertial or fictitious force that acts on objects in motion within a frame of reference that rotates with respect to an inertial frame. In a reference frame with clockwise rotation, the force acts to the ...
, the centrifugal force
In Newtonian mechanics, the centrifugal force is an inertial force (also called a "fictitious" or "pseudo" force) that appears to act on all objects when viewed in a rotating frame of reference. It is directed away from an axis which is paralle ...
(described below) and the Euler force In classical mechanics, the Euler force is the fictitious tangential force
that appears when a non-uniformly rotating reference frame is used for analysis of motion and there is variation in the angular velocity of the reference frame's axes. The E ...
. The Euler force is typically ignored because the variations in the angular velocity of the rotating surface of the Earth are usually insignificant. Both of the other fictitious forces are weak compared to most typical forces in everyday life, but they can be detected under careful conditions. For example, Léon Foucault
Jean Bernard Léon Foucault (, ; ; 18 September 1819 – 11 February 1868) was a French physicist best known for his demonstration of the Foucault pendulum, a device demonstrating the effect of Earth's rotation. He also made an early measurement ...
used his Foucault pendulum
The Foucault pendulum or Foucault's pendulum is a simple device named after French physicist Léon Foucault, conceived as an experiment to demonstrate the Earth's rotation. A long and heavy pendulum suspended from the high roof above a circular a ...
to show that a Coriolis force
In physics, the Coriolis force is an inertial or fictitious force that acts on objects in motion within a frame of reference that rotates with respect to an inertial frame. In a reference frame with clockwise rotation, the force acts to the ...
results from the Earth's rotation.
If the Earth were to rotate twenty times faster (making each day only ~72 minutes long), people could easily get the impression that such fictitious forces were pulling on them, as on a spinning carousel; people in temperate and tropical latitudes would, in fact, need to hold on in order to avoid being launched into orbit by the centrifugal force.
Detection of non-inertial reference frame
Observers inside a closed box that is moving with a constantvelocity
Velocity is the directional speed of an object in motion as an indication of its rate of change in position as observed from a particular frame of reference and as measured by a particular standard of time (e.g. northbound). Velocity is a ...
cannot detect their own motion; however, observers within an accelerating reference frame can detect that they are in a non-inertial reference frame from the fictitious forces that arise. For example, for straight-line acceleration Vladimir Arnold
Vladimir Igorevich Arnold (alternative spelling Arnol'd, russian: link=no, Влади́мир И́горевич Арно́льд, 12 June 1937 – 3 June 2010) was a Soviet and Russian mathematician. While he is best known for the Kolmogorov–A ...
presents the following theorem:
Other accelerations also give rise to fictitious forces, as described mathematically below
Below may refer to:
*Earth
*Ground (disambiguation)
*Soil
*Floor
*Bottom (disambiguation)
Bottom may refer to:
Anatomy and sex
* Bottom (BDSM), the partner in a BDSM who takes the passive, receiving, or obedient role, to that of the top or ...
. The physical explanation of motions in an inertial frame is the simplest possible, requiring no fictitious forces: fictitious forces are zero, providing a means to distinguish inertial frames from others.As part of the requirement of simplicity, to be an inertial frame, in all other frames that differ only by a uniform rate of translation, the description should be of the same form. However, in the Newtonian system the Galilean transformation
In physics, a Galilean transformation is used to transform between the coordinates of two reference frames which differ only by constant relative motion within the constructs of Newtonian physics. These transformations together with spatial rotatio ...
connects these frames and in the special theory of relativity the Lorentz transformation
In physics, the Lorentz transformations are a six-parameter family of linear transformations from a coordinate frame in spacetime to another frame that moves at a constant velocity relative to the former. The respective inverse transformation i ...
connects them. The two transformations agree for speeds of translation much less than the speed of light
The speed of light in vacuum, commonly denoted , is a universal physical constant that is important in many areas of physics. The speed of light is exactly equal to ). According to the special theory of relativity, is the upper limit ...
.
An example of the detection of a non-inertial, rotating reference frame is the precession of a Foucault pendulum
The Foucault pendulum or Foucault's pendulum is a simple device named after French physicist Léon Foucault, conceived as an experiment to demonstrate the Earth's rotation. A long and heavy pendulum suspended from the high roof above a circular a ...
. In the non-inertial frame of the Earth, the fictitious Coriolis force
In physics, the Coriolis force is an inertial or fictitious force that acts on objects in motion within a frame of reference that rotates with respect to an inertial frame. In a reference frame with clockwise rotation, the force acts to the ...
is necessary to explain observations. In an inertial frame outside the Earth, no such fictitious force is necessary.
Example concerning Circular motion
 The effect of a fictitious force also occurs when a car takes
The effect of a fictitious force also occurs when a car takes the bend
Wyntoon is the name of a private estate in rural Siskiyou County, California, owned by the Hearst Corporation. Architects Willis Polk, Bernard Maybeck and Julia Morgan all designed structures for Wyntoon, beginning in 1899.
The land, sited a ...
. Observed from a non-inertial frame of reference attached to the car, the fictitious force called the centrifugal force
In Newtonian mechanics, the centrifugal force is an inertial force (also called a "fictitious" or "pseudo" force) that appears to act on all objects when viewed in a rotating frame of reference. It is directed away from an axis which is paralle ...
appears. As the car enters a left turn, a suitcase first on the left rear seat slides to the right rear seat and then continues until it comes into contact with the closed door on the right. This motion marks the phase of the fictitious centrifugal force as it is the inertia of the suitcase which plays a role in this piece of movement. It may seem that there must be a force responsible for this movement, but actually, this movement arises because of the inertia of the suitcase, which is (still) a 'free object' within an already accelerating frame of reference.
After the suitcase has come into contact with the closed door of the car, the situation with the emergence of contact forces becomes current. The centripetal force on the car is now also transferred to the suitcase and the situation of Newton's third law comes into play, with the centripetal force as the action part and with the so-called reactive centrifugal force
In classical mechanics, a reactive centrifugal force forms part of an action–reaction pair with a centripetal force.
In accordance with Newton's first law of motion, an object moves in a straight line in the absence of a net force acting on th ...
as the reaction part. The reactive centrifugal force is also due to the inertia
Inertia is the idea that an object will continue its current motion until some force causes its speed or direction to change. The term is properly understood as shorthand for "the principle of inertia" as described by Newton in his first law ...
of the suitcase. Now however the inertia appears in the form of a manifesting resistance to a change in its state of motion.
Suppose a few miles further the car is moving at constant speed travelling a roundabout, again and again, then the occupants will feel as if they are being pushed to the outside of the vehicle by the (reactive) centrifugal force, away from the centre of the turn.
The situation can be viewed from inertial as well as from non-inertial frames.
* From the viewpoint of an inertial reference frame stationary with respect to the road, the car is accelerating toward the centre of the circle. It is accelerating, because the ''direction'' of the velocity is changing, despite the car having constant speed. This inward acceleration is called centripetal acceleration
In mechanics, acceleration is the rate of change of the velocity of an object with respect to time. Accelerations are vector quantities (in that they have magnitude and direction). The orientation of an object's acceleration is given by the ...
, it requires a centripetal force
A centripetal force (from Latin ''centrum'', "center" and ''petere'', "to seek") is a force that makes a body follow a curved path. Its direction is always orthogonal to the motion of the body and towards the fixed point of the instantaneous c ...
to maintain the circular motion. This force is exerted by the ground upon the wheels, in this case, from the friction
Friction is the force resisting the relative motion of solid surfaces, fluid layers, and material elements sliding against each other. There are several types of friction:
*Dry friction is a force that opposes the relative lateral motion of t ...
between the wheels and the road. The car is accelerating, due to the unbalanced force, which causes it to move in a circle. (See also banked turn
A banked turn (or banking turn) is a turn or change of direction in which the vehicle banks or inclines, usually towards the inside of the turn. For a road or railroad this is usually due to the roadbed having a transverse down-slope towards the ...
.)
* From the viewpoint of a rotating frame, moving with the car, a fictitious centrifugal force appears to be present pushing the car toward the outside of the road (and pushing the occupants toward the outside of the car). The centrifugal force balances the friction between wheels and the road, making the car stationary in this non-inertial frame.
A classic example of a fictitious force in circular motion is the experiment of rotating spheres
Isaac Newton's rotating spheres argument attempts to demonstrate that true rotational motion can be defined by observing the tension in the string joining two identical spheres. The basis of the argument is that all observers make two observation ...
tied by a cord and spinning around their centre of mass. In this case, the identification of a rotating, non-inertial frame of reference can be based upon the vanishing of fictitious forces. In an inertial frame, fictitious forces are not necessary to explain the tension in the string joining the spheres. In a rotating frame, Coriolis and centrifugal forces must be introduced to predict the observed tension.
In the rotating reference frame perceived on the surface of the Earth, a centrifugal force reduces the apparent force of gravity by about one part in a thousand, depending on latitude. This reduction is zero at the poles, maximum at the equator
The equator is a circle of latitude, about in circumference, that divides Earth into the Northern and Southern hemispheres. It is an imaginary line located at 0 degrees latitude, halfway between the North and South poles. The term can als ...
.
:
The fictitious Coriolis force
In physics, the Coriolis force is an inertial or fictitious force that acts on objects in motion within a frame of reference that rotates with respect to an inertial frame. In a reference frame with clockwise rotation, the force acts to the ...
, which is observed in rotational frames, is ordinarily visible only in very large-scale motion like the projectile motion of long-range guns or the circulation of the Earth's atmosphere (see Rossby number
The Rossby number (Ro), named for Carl-Gustav Arvid Rossby, is a dimensionless number used in describing fluid flow. The Rossby number is the ratio of inertial force to Coriolis force, terms , \mathbf \cdot \nabla \mathbf, \sim U^2 / L and \Omega ...
). Neglecting air resistance, an object dropped from a 50-meter-high tower at the equator will fall 7.7 millimetres eastward of the spot below where it is dropped because of the Coriolis force.
Fictitious forces and work
Fictitious forces can be considered to dowork
Work may refer to:
* Work (human activity), intentional activity people perform to support themselves, others, or the community
** Manual labour, physical work done by humans
** House work, housework, or homemaking
** Working animal, an animal tr ...
, provided that they move an object on a trajectory
A trajectory or flight path is the path that an object with mass in motion follows through space as a function of time. In classical mechanics, a trajectory is defined by Hamiltonian mechanics via canonical coordinates; hence, a complete traj ...
that changes its energy
In physics, energy (from Ancient Greek: ἐνέργεια, ''enérgeia'', “activity”) is the quantitative property that is transferred to a body or to a physical system, recognizable in the performance of work and in the form of heat a ...
from potential
Potential generally refers to a currently unrealized ability. The term is used in a wide variety of fields, from physics to the social sciences to indicate things that are in a state where they are able to change in ways ranging from the simple re ...
to kinetic
Kinetic (Ancient Greek: κίνησις “kinesis”, movement or to move) may refer to:
* Kinetic theory of gases, Kinetic theory, describing a gas as particles in random motion
* Kinetic energy, the energy of an object that it possesses due to i ...
. For example, consider some persons in rotating chairs holding a weight in their outstretched hands. If they pull their hand inward toward their body, from the perspective of the rotating reference frame, they have done work against the centrifugal force. When the weight is let go, it spontaneously flies outward relative to the rotating reference frame, because the centrifugal force does work on the object, converting its potential energy into kinetic. From an inertial viewpoint, of course, the object flies away from them because it is suddenly allowed to move in a straight line. This illustrates that the work done, like the total potential and kinetic energy of an object, can be different in a non-inertial frame than in an inertial one.
Gravity as a fictitious force
The notion of "fictitious force" comes up in Einstein's general theory of relativity. All fictitious forces are proportional to the mass of the object upon which they act, which is also true forgravity
In physics, gravity () is a fundamental interaction which causes mutual attraction between all things with mass or energy. Gravity is, by far, the weakest of the four fundamental interactions, approximately 1038 times weaker than the stro ...
.
The gravitational mass and the inertial mass are found experimentally to be equal to each other within experimental error. This led Albert Einstein
Albert Einstein ( ; ; 14 March 1879 – 18 April 1955) was a German-born theoretical physicist, widely acknowledged to be one of the greatest and most influential physicists of all time. Einstein is best known for developing the theory ...
to wonder whether gravity was a fictitious force as well. He noted that a freefall
In Newtonian physics, free fall is any motion of a body where gravity is the only force acting upon it. In the context of general relativity, where gravitation is reduced to a space-time curvature, a body in free fall has no force acting on it. ...
ing observer in a closed box would not be able to detect the force of gravity; hence, freefalling reference frames are equivalent to an inertial reference frame (the equivalence principle
In the theory of general relativity, the equivalence principle is the equivalence of gravitational and inertial mass, and Albert Einstein's observation that the gravitational "force" as experienced locally while standing on a massive body (suc ...
). Following up on this insight, Einstein formulated a theory with gravity as a fictitious force and attributed the apparent acceleration of gravity to the curvature
In mathematics, curvature is any of several strongly related concepts in geometry. Intuitively, the curvature is the amount by which a curve deviates from being a straight line, or a surface deviates from being a plane.
For curves, the canonic ...
of spacetime
In physics, spacetime is a mathematical model that combines the three dimensions of space and one dimension of time into a single four-dimensional manifold. Spacetime diagrams can be used to visualize relativistic effects, such as why differen ...
. This idea underlies Einstein's theory of general relativity
General relativity, also known as the general theory of relativity and Einstein's theory of gravity, is the geometric theory of gravitation published by Albert Einstein in 1915 and is the current description of gravitation in modern physics ...
. See Eötvös experiment
The Eötvös experiment was a famous physics experiment that measured the correlation between inertial mass and gravitational mass, demonstrating that the two were one and the same, something that had long been suspected but never demonstrated with ...
.
:
Mathematical derivation of fictitious forces
General derivation
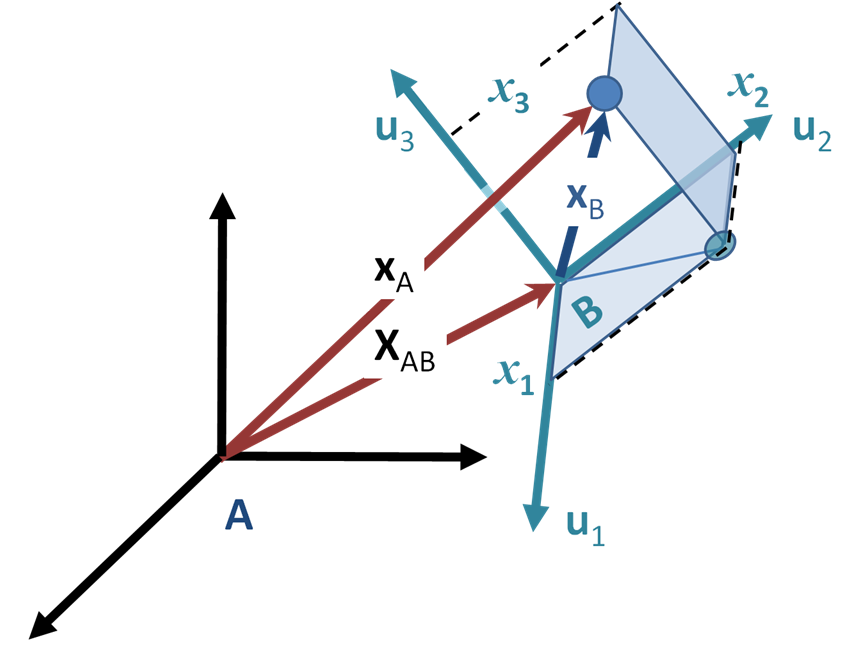
Many problems require use of noninertial reference frames, for example, those involving satellites and particle accelerators. Figure 2 shows a particle withmass
Mass is an intrinsic property of a body. It was traditionally believed to be related to the quantity of matter in a physical body, until the discovery of the atom and particle physics. It was found that different atoms and different elementar ...
''m'' and position
Position often refers to:
* Position (geometry), the spatial location (rather than orientation) of an entity
* Position, a job or occupation
Position may also refer to:
Games and recreation
* Position (poker), location relative to the dealer
* ...
vector
Vector most often refers to:
*Euclidean vector, a quantity with a magnitude and a direction
*Vector (epidemiology), an agent that carries and transmits an infectious pathogen into another living organism
Vector may also refer to:
Mathematic ...
xA(''t'') in a particular inertial frame
In classical physics and special relativity, an inertial frame of reference (also called inertial reference frame, inertial frame, inertial space, or Galilean reference frame) is a frame of reference that is not undergoing any acceleration. ...
A. Consider a non-inertial frame B whose origin relative to the inertial one is given by XAB(''t''). Let the position of the particle in frame B be xB(''t''). What is the force on the particle as expressed in the coordinate system of frame B?
To answer this question, let the coordinate axis in B be represented by unit vectors u''j'' with ''j'' any of for the three coordinate axes. Then
:
The interpretation of this equation is that xB is the vector displacement of the particle as expressed in terms of the coordinates in frame B at the time ''t''. From frame A the particle is located at:
:
As an aside, the unit vectors cannot change magnitude, so derivatives of these vectors express only rotation of the coordinate system B. On the other hand, vector XAB simply locates the origin of frame B relative to frame A, and so cannot include rotation of frame B.
Taking a time derivative, the velocity of the particle is:
:
The second term summation is the velocity of the particle, say vB as measured in frame B. That is:
:
The interpretation of this equation is that the velocity of the particle seen by observers in frame A consists of what observers in frame B call the velocity, namely vB, plus two extra terms related to the rate of change of the frame-B coordinate axes. One of these is simply the velocity of the moving origin vAB. The other is a contribution to velocity due to the fact that different locations in the non-inertial frame have different apparent velocities due to the rotation of the frame; a point seen from a rotating frame has a rotational component of velocity that is greater the further the point is from the origin.
To find the acceleration, another time differentiation provides:
:
Using the same formula already used for the time derivative of xB, the velocity derivative on the right is:
:
Consequently,
The interpretation of this equation is as follows: the acceleration of the particle in frame A consists of what observers in frame B call the particle acceleration aB, but in addition, there are three acceleration terms related to the movement of the frame-B coordinate axes: one term related to the acceleration of the origin of frame B, namely aAB, and two terms related to the rotation of frame B. Consequently, observers in B will see the particle motion as possessing "extra" acceleration, which they will attribute to "forces" acting on the particle, but which observers in A say are "fictitious" forces arising simply because observers in B do not recognize the non-inertial nature of frame B.
The factor of two in the Coriolis force arises from two equal contributions: (i) the apparent change of an inertially constant velocity with time because rotation makes the direction of the velocity seem to change (a ''d''vB/d''t'' term) and (ii) an apparent change in the velocity of an object when its position changes, putting it nearer to or further from the axis of rotation (the change in due to change in ''x j'' ).
To put matters in terms of forces, the accelerations are multiplied by the particle mass:
:
The force observed in frame B, FB = ''m''aB is related to the actual force on the particle, FA, by
:
where:
:
Thus, problems may be solved in frame B by assuming that Newton's second law holds (with respect to quantities in that frame) and treating Ffictitious as an additional force.
Below are a number of examples applying this result for fictitious forces. More examples can be found in the article on centrifugal force
In Newtonian mechanics, the centrifugal force is an inertial force (also called a "fictitious" or "pseudo" force) that appears to act on all objects when viewed in a rotating frame of reference. It is directed away from an axis which is paralle ...
.
Rotating coordinate systems
A common situation in which noninertial reference frames are useful is when the reference frame is rotating. Because such rotational motion is non-inertial, due to the acceleration present in any rotational motion, a fictitious force can always be invoked by using a rotational frame of reference. Despite this complication, the use of fictitious forces often simplifies the calculations involved. To derive expressions for the fictitious forces, derivatives are needed for the apparent time rate of change of vectors that take into account time-variation of the coordinate axes. If the rotation of frame 'B' is represented by a vector Ω pointed along the axis of rotation with the orientation given by theright-hand rule
In mathematics and physics, the right-hand rule is a common mnemonic for understanding orientation of axes in three-dimensional space. It is also a convenient method for quickly finding the direction of a cross-product of 2 vectors.
Most of th ...
, and with magnitude given by
:
then the time derivative of any of the three unit vectors describing frame B is
:
and
:
as is verified using the properties of the vector cross product
In mathematics, the cross product or vector product (occasionally directed area product, to emphasize its geometric significance) is a binary operation on two vectors in a three-dimensional oriented Euclidean vector space (named here E), and is ...
. These derivative formulas now are applied to the relationship between acceleration in an inertial frame, and that in a coordinate frame rotating with time-varying angular velocity ω(''t''). From the previous section, where subscript A refers to the inertial frame and B to the rotating frame, setting aAB = 0 to remove any translational acceleration, and focusing on only rotational properties (see Eq. 1):
:
:
Collecting terms, the result is the so-called ''acceleration transformation formula'':
:
The physical acceleration aA due to what observers in the inertial frame A call ''real external forces'' on the object is, therefore, not simply the acceleration aB seen by observers in the rotational frame B, but has several additional geometric acceleration terms associated with the rotation of B. As seen in the rotational frame, the acceleration aB of the particle is given by rearrangement of the above equation as:
:
The net force upon the object according to observers in the rotating frame is FB = ''m''aB. If their observations are to result in the correct force on the object when using Newton's laws, they must consider that the additional force Ffict is present, so the end result is FB = FA + Ffict. Thus, the fictitious force used by observers in B to get the correct behaviour of the object from Newton's laws equals:
:
Here, the first term is the ''Coriolis force
In physics, the Coriolis force is an inertial or fictitious force that acts on objects in motion within a frame of reference that rotates with respect to an inertial frame. In a reference frame with clockwise rotation, the force acts to the ...
'', the second term is the ''centrifugal force
In Newtonian mechanics, the centrifugal force is an inertial force (also called a "fictitious" or "pseudo" force) that appears to act on all objects when viewed in a rotating frame of reference. It is directed away from an axis which is paralle ...
'', and the third term is the ''Euler force In classical mechanics, the Euler force is the fictitious tangential force
that appears when a non-uniformly rotating reference frame is used for analysis of motion and there is variation in the angular velocity of the reference frame's axes. The E ...
''.
Orbiting coordinate systems
Orbiting and rotating
barycenter
In astronomy, the barycenter (or barycentre; ) is the center of mass of two or more bodies that orbit one another and is the point about which the bodies orbit. A barycenter is a dynamical point, not a physical object. It is an important conc ...
, not the Earth's center; see In this example, unit vector u3 retains a fixed orientation, while vectors u1, u2 rotate at the same rate as the origin of coordinates. That is,
:
:
Hence, the acceleration of a moving object is expressed as (see Eq. 1):
:
where the angular acceleration term is zero for the constant rate of rotation.
Because the first term, which is
is of the same form as the normal centrifugal force expression:
it is a natural extension of standard terminology (although there is no standard terminology for this case) to call this term the "centrifugal force". Applying this terminology to the example of a tube in a centrifuge, if the tube is far enough from the center of rotation, , XAB, = ''R'' ≫ , xB, , all the matter in the test tube sees the same acceleration (the same centrifugal force). Thus, in this case, the fictitious force is primarily a uniform centrifugal force along the axis of the tube, away from the centre of rotation, with a value , Ffict, = ω2 ''R'', where ''R'' is the distance of the matter in the tube from the centre of the centrifuge. It is the standard specification of a centrifuge to use the "effective" radius of the centrifuge to estimate its ability to provide centrifugal force. Thus, the first estimate of centrifugal force in a centrifuge can be based upon the distance of the tubes from the centre of rotation, and corrections applied if needed.
Also, the test tube confines motion to the direction down the length of the tube, so vB is opposite to u1 and the Coriolis force is opposite to u2, that is, against the wall of the tube. If the tube is spun for a long enough time, the velocity vB drops to zero as the matter comes to an equilibrium distribution. For more details, see the articles on sedimentation
Sedimentation is the deposition of sediments. It takes place when particles in suspension settle out of the fluid in which they are entrained and come to rest against a barrier. This is due to their motion through the fluid in response to the ...
and the Lamm equation The Lamm equationO Lamm: (1929) "Die Differentialgleichung der Ultrazentrifugierung"'' Arkiv för matematik, astronomi och fysik'' 21B No. 2, 1–4 describes the sedimentation and diffusion of a solute under ultracentrifugation in traditional s ...
.
A related problem is that of centrifugal forces for the Earth–Moon–Sun system, where three rotations appear: the daily rotation of the Earth about its axis, the lunar-month rotation of the Earth–Moon system about its centre of mass, and the annual revolution of the Earth–Moon system about the Sun. These three motions influence the tide
Tides are the rise and fall of sea levels caused by the combined effects of the gravity, gravitational forces exerted by the Moon (and to a much lesser extent, the Sun) and are also caused by the Earth and Moon orbiting one another.
Tide t ...
s.
Crossing a carousel
carousel
A carousel or carrousel (mainly North American English), merry-go-round (List of sovereign states, international), roundabout (British English), or hurdy-gurdy (an old term in Australian English, in South Australia, SA) is a type of amusement ...
.For a similar example, see , and The carousel rotates at a constant angular velocity represented by the vector Ω with magnitude ''ω'', pointing upward according to the right-hand rule
In mathematics and physics, the right-hand rule is a common mnemonic for understanding orientation of axes in three-dimensional space. It is also a convenient method for quickly finding the direction of a cross-product of 2 vectors.
Most of th ...
. A rider on the carousel walks radially across it at a constant speed, in what appears to the walker to be the straight line path inclined at 45° in Figure 5. To the stationary observer, however, the walker travels a spiral path. The points identified on both paths in Figure 5 correspond to the same times spaced at equal time intervals. We ask how two observers, one on the carousel and one in an inertial frame, formulate what they see using Newton's laws.
Inertial observer
The observer at rest describes the path followed by the walker as a spiral. Adopting the coordinate system shown in Figure 5, the trajectory is described by r(''t''): : where the added π/4 sets the path angle at 45° to start with (just an arbitrary choice of direction), u''R'' is a unit vector in the radial direction pointing from the centre of the carousel to the walker at the time ''t''. The radial distance ''R''(''t'') increases steadily with time according to: : with ''s'' the speed of walking. According to simple kinematics, the velocity is then the first derivative of the trajectory: : with uθ a unit vector perpendicular to uR at time ''t'' (as can be verified by noticing that the vectordot product
In mathematics, the dot product or scalar productThe term ''scalar product'' means literally "product with a scalar as a result". It is also used sometimes for other symmetric bilinear forms, for example in a pseudo-Euclidean space. is an algebra ...
with the radial vector is zero) and pointing in the direction of travel.
The acceleration is the first derivative of the velocity:
:
The last term in the acceleration is radially inward of magnitude ω2 ''R'', which is therefore the instantaneous centripetal acceleration
In mechanics, acceleration is the rate of change of the velocity of an object with respect to time. Accelerations are vector quantities (in that they have magnitude and direction). The orientation of an object's acceleration is given by the ...
of circular motion
In physics, circular motion is a movement of an object along the circumference of a circle or rotation along a circular path. It can be uniform, with constant angular rate of rotation and constant speed, or non-uniform with a changing rate of ro ...
. The first term is perpendicular to the radial direction, and pointing in the direction of travel. Its magnitude is 2''sω'', and it represents the acceleration of the walker as the edge of the carousel is neared, and the arc of the circle travelled in a fixed time increases, as can be seen by the increased spacing between points for equal time steps on the spiral in Figure 5 as the outer edge of the carousel is approached.
Applying Newton's laws, multiplying the acceleration by the mass of the walker, the inertial observer concludes that the walker is subject to two forces: the inward radially directed centripetal force and another force perpendicular to the radial direction that is proportional to the speed of the walker.
Rotating observer
The rotating observer sees the walker travel a straight line from the centre of the carousel to the periphery, as shown in Figure 5. Moreover, the rotating observer sees that the walker moves at a constant speed in the same direction, so applying Newton's law of inertia, there is ''zero'' force upon the walker. These conclusions do not agree with the inertial observer. To obtain agreement, the rotating observer has to introduce fictitious forces that appear to exist in the rotating world, even though there is no apparent reason for them, no apparent gravitational mass, electric charge or what have you, that could account for these fictitious forces. To agree with the inertial observer, the forces applied to the walker must be exactly those found above. They can be related to the general formulas already derived, namely: : In this example, the velocity seen in the rotating frame is: : with uR a unit vector in the radial direction. The position of the walker as seen on the carousel is: : and the time derivative of Ω is zero for uniform angular rotation. Noticing that : and : we find: : To obtain a straight-line motion in the rotating world, a force exactly opposite in sign to the fictitious force must be applied to reduce the net force on the walker to zero, so Newton's law of inertia will predict a straight line motion, in agreement with what the rotating observer sees. The fictitious forces that must be combated are theCoriolis force
In physics, the Coriolis force is an inertial or fictitious force that acts on objects in motion within a frame of reference that rotates with respect to an inertial frame. In a reference frame with clockwise rotation, the force acts to the ...
(first term) and the centrifugal force
In Newtonian mechanics, the centrifugal force is an inertial force (also called a "fictitious" or "pseudo" force) that appears to act on all objects when viewed in a rotating frame of reference. It is directed away from an axis which is paralle ...
(second term). (These terms are approximate.A circle about the axis of rotation is not the osculating circle
In differential geometry of curves, the osculating circle of a sufficiently smooth plane curve at a given point ''p'' on the curve has been traditionally defined as the circle passing through ''p'' and a pair of additional points on the curve i ...
of the walker's trajectory, so "centrifugal" and "Coriolis" are approximate uses for these terms. See note.) By applying forces to counter these two fictitious forces, the rotating observer ends up applying exactly the same forces upon the walker that the inertial observer predicted were needed.
Because they differ only by the constant walking velocity, the walker and the rotational observer see the same accelerations. From the walker's perspective, the fictitious force is experienced as real, and combating this force is necessary to stay on a straight line radial path holding a constant speed. It's like battling a crosswind while being thrown to the edge of the carousel.
In this connection, it may be noted that a change in the coordinate system, for example, from Cartesian to polar, if implemented without any change in relative motion, does not cause the appearance of rotational fictitious forces, despite the fact that the form of the laws of motion varies from one type of curvilinear coordinate system to another, depending from the (purely spatial) delta-curvature: , where are the contravariant components of the force per unit mass, and are the Christoffel symbols
In mathematics and physics, the Christoffel symbols are an array of numbers describing a metric connection. The metric connection is a specialization of the affine connection to surfaces or other manifolds endowed with a metric, allowing distance ...
of the second kind, see, for instance: David, Kay, ''Tensor Calculus'' (1988) McGraw-Hill Book Company , Section 11.4; or: Adler, R., Bazin, M., & Schiffer, M. ''Introduction to General Relativity'' (New York, 1965). This could be the first hint of the crisis of the non-relativistic physics: in "non-inertial" frames using non-Euclidean and not flat metrics, fictitious forces transform into force exchanged with "objects" that do not follow the geodesic trajectory (simply with a relative speed respect it). In any case this generalized "Newton's second law" must wait for the general relativity
General relativity, also known as the general theory of relativity and Einstein's theory of gravity, is the geometric theory of gravitation published by Albert Einstein in 1915 and is the current description of gravitation in modern physics ...
to obtain curvature in spacetime according to stress–energy tensor
The stress–energy tensor, sometimes called the stress–energy–momentum tensor or the energy–momentum tensor, is a tensor physical quantity that describes the density and flux of energy and momentum in spacetime, generalizing the stress ...
by Einstein field equations
In the general theory of relativity, the Einstein field equations (EFE; also known as Einstein's equations) relate the geometry of spacetime to the distribution of matter within it.
The equations were published by Einstein in 1915 in the form ...
and a spacetime form that uses the four-force In the special theory of relativity, four-force is a four-vector that replaces the classical force.
In special relativity
The four-force is defined as the rate of change in the four-momentum of a particle with respect to the particle's proper ti ...
density tensor that is derived from the covariant divergence of the energy-momentum tensor.
Observation
Notice that thiskinematical
Kinematics is a subfield of physics, developed in classical mechanics, that describes the motion of points, bodies (objects), and systems of bodies (groups of objects) without considering the forces that cause them to move. Kinematics, as a fiel ...
discussion does not delve into the mechanism by which the required forces are generated. That is the subject of kinetics
Kinetics ( grc, κίνησις, , kinesis, ''movement'' or ''to move'') may refer to:
Science and medicine
* Kinetics (physics), the study of motion and its causes
** Rigid body kinetics, the study of the motion of rigid bodies
* Chemical ki ...
. In the case of the carousel, the kinetic discussion would involve perhaps a study of the walker's shoes and the friction they need to generate against the floor of the carousel, or perhaps the dynamics of skateboarding if the walker switched to travel by skateboard. Whatever the means of travel across the carousel, the forces calculated above must be realized. A very rough analogy is heating your house: you must have a certain temperature to be comfortable, but whether you heat by burning gas or by burning coal is another problem. Kinematics sets the thermostat, kinetics fires the furnace.
See also
*Analytical mechanics
In theoretical physics and mathematical physics, analytical mechanics, or theoretical mechanics is a collection of closely related alternative formulations of classical mechanics. It was developed by many scientists and mathematicians during the ...
* Applied mechanics
Applied mechanics is the branch of science concerned with the motion of any substance that can be experienced or perceived by humans without the help of instruments. In short, when mechanics concepts surpass being theoretical and are applied and e ...
* Centrifugal force
In Newtonian mechanics, the centrifugal force is an inertial force (also called a "fictitious" or "pseudo" force) that appears to act on all objects when viewed in a rotating frame of reference. It is directed away from an axis which is paralle ...
* Centripetal force
A centripetal force (from Latin ''centrum'', "center" and ''petere'', "to seek") is a force that makes a body follow a curved path. Its direction is always orthogonal to the motion of the body and towards the fixed point of the instantaneous c ...
* Circular motion
In physics, circular motion is a movement of an object along the circumference of a circle or rotation along a circular path. It can be uniform, with constant angular rate of rotation and constant speed, or non-uniform with a changing rate of ro ...
* Classical mechanics
Classical mechanics is a physical theory describing the motion of macroscopic objects, from projectiles to parts of machinery, and astronomical objects, such as spacecraft, planets, stars, and galaxies. For objects governed by classical ...
* Coriolis force
In physics, the Coriolis force is an inertial or fictitious force that acts on objects in motion within a frame of reference that rotates with respect to an inertial frame. In a reference frame with clockwise rotation, the force acts to the ...
* Curvilinear coordinates
In geometry, curvilinear coordinates are a coordinate system for Euclidean space in which the coordinate lines may be curved. These coordinates may be derived from a set of Cartesian coordinates by using a transformation that is locally inve ...
* d'Alembert's principle
D'Alembert's principle, also known as the Lagrange–d'Alembert principle, is a statement of the fundamental classical laws of motion. It is named after its discoverer, the French physicist and mathematician Jean le Rond d'Alembert. D'Alember ...
of inertial forces
* Dynamics (physics)
Dynamics is the branch of classical mechanics that is concerned with the study of forces and their effects on motion. Isaac Newton was the first to formulate the fundamental physical laws that govern dynamics in classical non-relativistic physi ...
* Free motion equation A free motion equation is a differential equation that describes a mechanical system in the absence of external forces, but in the presence only of an inertial force depending on the choice of a reference frame.
In non-autonomous mechanics on a con ...
* Frenet–Serret formulas
In differential geometry, the Frenet–Serret formulas describe the kinematic properties of a particle moving along a differentiable curve in three-dimensional Euclidean space \mathbb^, or the geometric properties of the curve itself irrespective ...
* General relativity
General relativity, also known as the general theory of relativity and Einstein's theory of gravity, is the geometric theory of gravitation published by Albert Einstein in 1915 and is the current description of gravitation in modern physics ...
* Generalized coordinates
In analytical mechanics, generalized coordinates are a set of parameters used to represent the state of a system in a configuration space. These parameters must uniquely define the configuration of the system relative to a reference state.,p. 3 ...
* Generalized force Generalized forces find use in Lagrangian mechanics, where they play a role conjugate to generalized coordinates. They are obtained from the applied forces, Fi, i=1,..., n, acting on a system that has its configuration defined in terms of generali ...
* Gravity
In physics, gravity () is a fundamental interaction which causes mutual attraction between all things with mass or energy. Gravity is, by far, the weakest of the four fundamental interactions, approximately 1038 times weaker than the stro ...
* Inertial reference frame
In classical physics and special relativity, an inertial frame of reference (also called inertial reference frame, inertial frame, inertial space, or Galilean reference frame) is a frame of reference that is not undergoing any acceleration. ...
* Kinematics
Kinematics is a subfield of physics, developed in classical mechanics, that describes the Motion (physics), motion of points, Physical object, bodies (objects), and systems of bodies (groups of objects) without considering the forces that cause ...
* Kinetics (physics)
In physics and engineering, kinetics is the branch of classical mechanics that is concerned with the relationship between the motion and its causes, specifically, forces and torques. Since the mid-20th century, the term " dynamics" (or "analytic ...
* Newton's laws of motion
Newton's laws of motion are three basic laws of classical mechanics that describe the relationship between the motion of an object and the forces acting on it. These laws can be paraphrased as follows:
# A body remains at rest, or in moti ...
* Non-inertial reference frame
A non-inertial reference frame is a frame of reference that undergoes acceleration with respect to an inertial frame. An accelerometer at rest in a non-inertial frame will, in general, detect a non-zero acceleration. While the laws of motion are ...
* Orthogonal coordinates In mathematics, orthogonal coordinates are defined as a set of ''d'' coordinates q = (''q''1, ''q''2, ..., ''q'd'') in which the coordinate hypersurfaces all meet at right angles (note: superscripts are indices, not exponents). A coordinate su ...
* Rotating reference frame
A rotating frame of reference is a special case of a non-inertial reference frame that is rotating relative to an inertial reference frame. An everyday example of a rotating reference frame is the surface of the Earth. (This article considers onl ...
* Statics
Statics is the branch of classical mechanics that is concerned with the analysis of force and torque (also called moment) acting on physical systems that do not experience an acceleration (''a''=0), but rather, are in static equilibrium with ...
* Uniform circular motion
In physics, circular motion is a movement of an object along the circumference of a circle or rotation along a circular path. It can be uniform, with constant angular rate of rotation and constant speed, or non-uniform with a changing rate of rot ...
Notes
Further reading
* * * *External links
Q and A from Richard C. Brill, Honolulu Community College
* ttps://scienceworld.wolfram.com/physics/CoriolisForce.html Coriolis Force
Motion over a flat surface
Java physlet by Brian Fiedler illustrating fictitious forces. The physlet shows both the perspective as seen from a rotating and from a non-rotating point of view.
Java physlet by Brian Fiedler illustrating fictitious forces. The physlet shows both the perspective as seen from a rotating and as seen from a non-rotating point of view. {{Authority control Classical mechanics Force